Tutorial 9: Engineering Applications of Integral

Q1: Find the arc length \(L\) of the curve \(y=x^{\frac{3}{2}}\) from \(x=0\) to \(x=5\).

Solution

\[y' =\frac{3}{2} x^{\frac{1}{2}} =\frac{3}{2}\sqrt{x}\] \[\begin{aligned} L & =\int _{0}^{5}\sqrt{1+( y')^{2}} \ dx\\ & =\int _{0}^{5}\sqrt{1+\left(\frac{3}{2}\sqrt{x}\right)^{2}} \ dx\\ & =\int _{0}^{5}\sqrt{1+\frac{9}{4} x} \ dx\\ & =\int _{0}^{5}\left( 1+\frac{9}{4} x\right)^{\frac{1}{2}} \ dx\\ & =\left. \frac{\left( 1+\frac{9}{4} x\right)^{\frac{3}{2}}}{\left(\frac{3}{2}\right)\left(\frac{9}{4}\right)}\right| _{0}^{5}\\ & =\frac{\left( 1+\frac{9}{4}( 5)\right)^{\frac{3}{2}}}{\frac{27}{8}} -\frac{\left( 1+\frac{9}{4}( 0)\right)^{\frac{3}{2}}}{\frac{27}{8}}\\ & =\mathbf{\frac{335}{27}} \end{aligned}\]

Q2: Find the area bounded by the parabola \(x=8+2y-y^{2}\), the y-axis, and the lines \(y=-1\) and \(y=3\).

Solution

\[\begin{aligned} x & =8+2y-y^{2}\\ & =-\left( y^{2} -2y-8\right)\\ & =-\left(( y-1)^{2} -9\right)\\ & =( 4-y)( 2+y) \end{aligned}\]

\(\therefore\) The vortex of the parabola is \((9,1)\) and cuts the y-axis at \(y=-4\), \(y=-2\).

Area bounded by the parabola:

\[\begin{aligned} \int _{-1}^{3}\left( 8+2y-y^{2}\right) \ dy & =\left. 8y+y^{2} -\frac{1}{3} y^{3}\right| _{-1}^{3}\\ & =\left( 8( 3) +3^{2} -\frac{1}{3}( 3)^{3}\right) -\left( 8( -1) +( -1)^{2} -\frac{1}{3}( -1)^{3}\right)\\ & =\mathbf{\frac{92}{3}} \end{aligned}\]

Q3: Find the arc length of the catenary \(y=\frac{a}{2}\left( e^{\frac{x}{a}} +e^{-\frac{x}{a}}\right)\) from \(x=0\) to \(x=a\).

Solution

\[\begin{aligned} y' & =\frac{a}{2}\left(\frac{1}{a} e^{\frac{x}{a}} -\frac{1}{a} e^{-\frac{x}{a}}\right) +0\left( e^{\frac{x}{a}} +e^{-\frac{x}{a}}\right)\\ & =\frac{a}{2}\left(\frac{1}{a}\right)\left( e^{\frac{x}{a}} -e^{-\frac{x}{a}}\right)\\ & =\frac{1}{2}\left( e^{\frac{x}{a}} -e^{-\frac{x}{a}}\right) \end{aligned}\]

Arc length:

\[\begin{aligned} L & =\int _{0}^{a}\sqrt{1+( y')^{2}} \ dx\\ & =\int _{0}^{a}\sqrt{1+\left[\frac{1}{2}\left( e^{\frac{x}{a}} -e^{-\frac{x}{a}}\right)\right]^{2}} dx\\ & =\int _{0}^{a}\sqrt{1+\frac{1}{4}\left( e^{\frac{2x}{a}} -2e^{0} +e^{-\frac{2x}{a}}\right)} dx\\ & =\int _{0}^{a}\sqrt{1+\frac{1}{4} e^{\frac{2x}{a}} -\frac{1}{2} +\frac{1}{4} e^{-\frac{2x}{a}}} dx\\ & =\int _{0}^{a}\sqrt{\frac{1}{4} e^{\frac{2x}{a}} +\frac{1}{2} +\frac{1}{4} e^{-\frac{2x}{a}}} dx\\ & =\int _{0}^{a}\sqrt{\frac{1}{4}\left[ e^{\frac{2x}{a}} +2+ e^{-\frac{2x}{a}}\right]} dx\\ & =\int _{0}^{a}\sqrt{\frac{1}{4}\left( e^{\frac{x}{a}} +e^{-\frac{x}{a}}\right)^{2}} dx\\ & =\int _{0}^{a}\frac{1}{2}\left( e^{\frac{x}{a}} +e^{-\frac{x}{a}}\right) \ dx\\ & =\frac{1}{2}\int _{0}^{a}\left( e^{\frac{x}{a}} +e^{-\frac{x}{a}}\right) \ dx\\ & =\frac{1}{2}\left[\left. \frac{e^{\frac{x}{a}}}{\frac{1}{a}} -\frac{e^{-\frac{x}{a}}}{\frac{1}{a}}\right| _{0}^{a}\right]\\ & =\frac{1}{2} \div a\left[ e^{1} +e^{-1} -1+1\right]\\ & =\mathbf{\frac{a}{2}\left[ e-e^{-1}\right]} \end{aligned}\]

Q4: Find the centroid of the plane area bounded by the parabolas \(y=2x−x^{2}\) and \(y=3x^{2}-6x\).

Solution

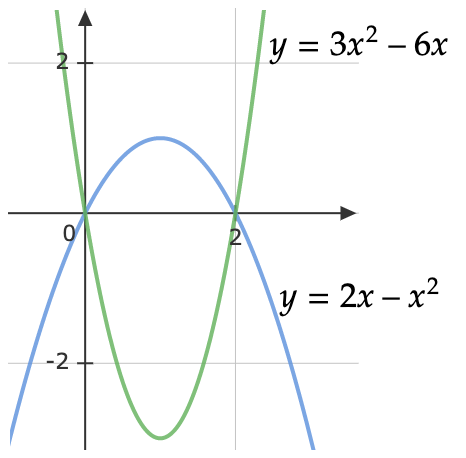
Graph for solution of Question 4

\[\begin{aligned} A & =\int \int\limits _{R} dA\\ & =\int _{0}^{2}\int _{3x^{2} -6x}^{2x-x^{2}} dydx\\ & =\int _{0}^{2}\left[ 2x-x^{2} -3x^{2} +6x\right] dx\\ & =\int _{0}^{2}\left[ -4x^{2} +8x\right] dx\\ & =\left. \frac{-4x^{3}}{3} +4x^{2}\right| _{0}^{2}\\ & =\frac{-4( 2)^{3}}{3} +4( 2)^{2}\\ & =\mathbf{\frac{16}{3}} \end{aligned}\] \[\begin{aligned} M_{y} & =\int \int\limits _{R} x\ dA\\ & =\int _{0}^{2}\int _{3x^{2} -6x}^{2x-x^{2}} x\ dydx\\ & =\int _{0}^{2} x\left( 2x-x^{2} -3x^{2} +6x\right) \ dx\\ & =\int _{0}^{2}\left[ -4x^{3} +8x^{2}\right] dx\\ & =\left. -x^{4} +\frac{8}{3} x^{3}\right| _{0}^{2}\\ & =-2^{4} +\frac{8}{3}( 2)^{3}\\ & =\mathbf{\frac{16}{3}} \end{aligned}\] \[\begin{aligned} M_{x} & =\int \int\limits _{R} y\ dA\\ & =\int _{0}^{2}\int _{3x^{2} -6x}^{2x-x^{2}} y\ dydx\\ & =\frac{1}{2}\int _{0}^{2}\left[\left( 2x-x^{2}\right)^{2} -\left( 3x^{2} -6x\right)^{2}\right] dx\\ & =\frac{1}{2}\int _{0}^{2}\left[ 4x^{2} -4x^{3} +x^{4} -9x^{4} +36x^{3} -36x^{2}\right] dx\\ & =\frac{1}{2}\int _{0}^{2}\left[ -8x^{4} +32x^{3} -32x^{2}\right] dx\\ & =\frac{1}{2}\left[\left. -\frac{8}{5} x^{5} +8x^{4} -\frac{32}{3} x^{3}\right| _{0}^{2}\right]\\ & =\frac{1}{2}\left[ -\frac{8}{5}( 2)^{5} +8( 2)^{4} -\frac{32}{3}( 2)^{3}\right]\\ & =-\frac{64}{15} \end{aligned}\]

Hence, \(x=\frac{M_{y}}{A} =\frac{\frac{16}{3}}{\frac{16}{3}} =1\), \(y=\frac{M_{x}}{A} =\frac{-\frac{64}{15}}{\frac{16}{3}} =-\frac{4}{5}\). Thus, the centroid is \(\left( 1,-\frac{4}{5}\right)\).

Q5: Find the hydrostatic force on a circular plate of radius 2 that is submerged 6 meters in the water.

Solution

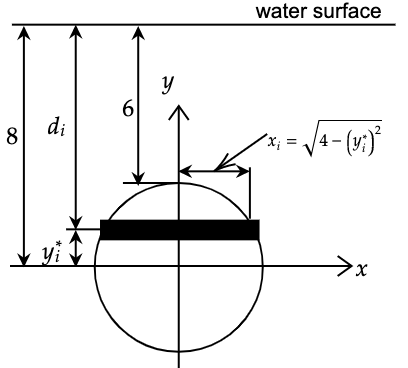
Graph for solution of Question 5

Assume that the top of the circular plate is 6 meters under the water.

Setting up the axis system such that the origin of the axis is at the center of the plate.

Finally, split up the plate into \(n\) horizontal strips each of width \(\Delta y\). Choosing a point \(y_{i}^{*}\) from each strip. Assume that the strips are rectangular.

The depth below the water surface of each strip is,

\[d_{i} =8-y_{i}^{*}\]

and that in turn gives us the pressure on the strip,

\[P_{i} =\rho gd_{i} =9810\left( 8-y_{i}^{*}\right)\]

The area of each strip is,

\[A_{i} =2\sqrt{4-\left( y_{i}^{*}\right)^{2}} \ \ \Delta y\]

The hydrostatic force on each strip is,

\[F_{i} =P_{i} A_{i} =9810\left( 8-y_{i}^{*}\right)( 2)\sqrt{4-\left( y_{i}^{*}\right)^{2}} \ \ \Delta y\]

The total force on the plate is,

\[\begin{aligned} F & =\lim\limits _{n\rightarrow \infty }\sum\limits _{i=1}^{n} 19620\left( 8-y_{i}^{*}\right)\sqrt{4-\left( y_{i}^{*}\right)^{2}} \ \ \Delta y\\ & =19620\int _{\ -2}^{\ 2}( 8-y)\sqrt{4-y^{2}} \ dy\\ & =19620\int _{\ -2}^{\ 2} 8\sqrt{4-y^{2}} \ dy-19620\int _{\ -2}^{\ 2} y\sqrt{4-y^{2}} \ dy \end{aligned}\]

The first integral requires the trig substitution \(y=2\sin \theta\) and the second integral needs the substitution \(v=4-y^{2}\).

\[\begin{align*} F & =627840\int _{\ -\pi /2\ }^{\ \pi /2\ }\cos^{2} \theta \ d\theta +9810\int _{\ 0}^{\ 0}\sqrt{v} \ dv\\ & =313920\int _{\ -\pi /2\ }^{\ \pi /2\ } 1+\cos( 2\theta ) \ d\theta +0\\ & =313920\left. \left( \theta +\frac{1}{2}\sin( 2\theta )\right)\right| _{-\pi /2}^{\pi /2}\\ & =\mathbf{313920\pi } \end{align*}\]