Tutorial 4: Vector Algebra I

Tutorial PDF

Class Recording

Q1: Graphical interpretation and the effect of scalar multiplication

(i) For the position vector \(\underset{\sim }{a} =\langle 2,4\rangle\), compute \(3\underset{\sim }{a}\), \(\frac{1}{2}\underset{\sim }{a}\), and \(-2\underset{\sim }{a}\). Sketch all four vectors on the same axis system. Discuss the effect of scalar multiplication on the magnitude and direction of the original vector.

(ii) Determine if the sets of vectors are parallel or not.

a. \(\underset{\sim }{a} =\langle 2,4,-1\rangle\), \(\underset{\sim }{b} =\langle -6,-12,3\rangle\)

b. \(\underset{\sim }{a} =\langle 4,10\rangle\), \(\underset{\sim }{b} =\langle 2,-9\rangle\)

(iii) Find unit vector that has the same direction \(\underset{\sim }{u} =\langle -5,2,1\rangle\)

Solution

Question (i)

\(3\underset{\sim }{a} =\langle 6,12\rangle\), \(\frac{1}{2}\underset{\sim }{a} =\langle 1,2\rangle\), \(-2\underset{\sim }{a} =\langle -4,-8\rangle\)

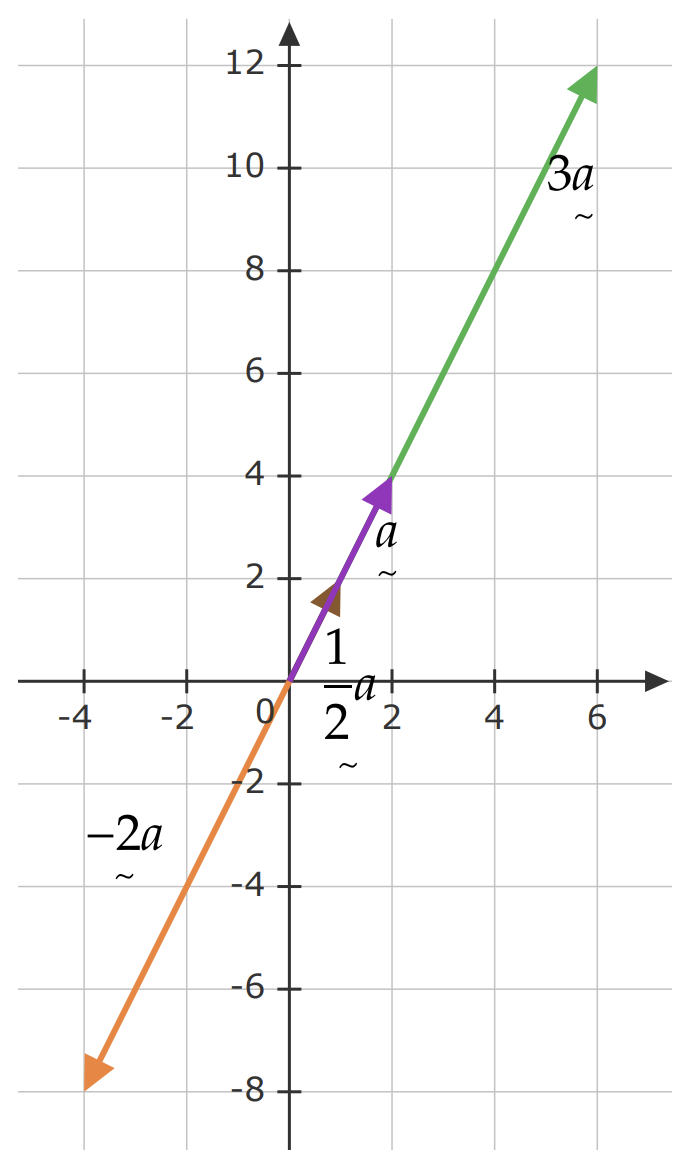
Graph for solution of Question 1(i)

The scalar multiplication affects the magnitude of vectors if the scalar is a negative value. For example, \(-2\underset{\sim }{a}\) switch the direction in exactly the opposite direction.
The scalar multiplication affects the magnitude of vectors if the scalar is not equal to 1.
When scalar > 1, the length of the vector is stretched. (magnitude increased)
When scalar < 1, the length of the vector is shrinked. (magnitude decteased)

Question (ii)

(a) These two vectors are parallel since \(\underset{\sim }{b} =-3\underset{\sim }{a}\).

(b) These two vectors are not parallel since there is no scalar that can fulfil the scalar multiplication.

Question (iii)

We use \(\widehat{\underset{\sim }{u}} =\frac{\underset{\sim }{u}}{\vert\underset{\sim }{u} \vert} =\frac{1}{\vert\underset{\sim }{u} \vert}\underset{\sim }{u}\).

The chosen scalar is \(\frac{1}{\underset{\sim }{u}}\) so when multiply to vector \(\underset{\sim }{u}\), which has magnitude of \(\vert\underset{\sim }{u} \vert\), a vector of magnitude 1 is obtained.

Besides, \(\widehat{\underset{\sim }{u}} \vert\vert\underset{\sim }{u}\) as scalar multiplication works within them.

Q2: Let \(A( 1,3,5)\) and \(B(4,6,2)\). Find the point \(C\) so that it is located on the line segment \(AB\) which divides \(AB\) into two segments which are in the ratio 1:3.

Solution

\[\begin{aligned} \underset{\sim }{c} & =\frac{1}{m+n}\left( n\underset{\sim }{a} +m\underset{\sim }{b}\right)\\ & =\frac{1}{1+3}\left( 3\underset{\sim }{a} +\underset{\sim }{b}\right)\\ & =\frac{1}{4}\left( 3\underset{\sim }{a} +\underset{\sim }{b}\right)\\ & =\frac{1}{4}( 3\langle 1,3,5\rangle +\langle 4,6,2\rangle )\\ & =\frac{1}{4} \langle 7,15,17\rangle \\ & =\mathbf{\langle \frac{7}{4} ,\frac{15}{4} ,\frac{17}{4} \rangle \ } \end{aligned}\]

Q3: Find the following equation of line for the line L passing through the point \(P( 3,1,\ -2)\) and \(Q( -2,7,\ -4)\).

(i) vector equation,

(ii) parametric equation, and

(iii) Cartesian equation

Solution

\(\overrightarrow{PQ} =\overrightarrow{OQ} -\overrightarrow{OP} =\langle -2,7,-4\rangle -\langle 3,1,-2\rangle =\langle -5,6,-2\rangle\) is a vector parallel to line \(L\)

Question (i)

\(\underset{\sim }{r} =\underset{\sim }{a} +t\underset{\sim }{v} =\langle 3,1,-2\rangle +t\langle -5,6,-2\rangle\) or \(r=\langle -2,7,-4\rangle +t\langle -5,6,-2\rangle\)

Question (ii)

Using \(\underset{\sim }{r} =\langle 3,1,-2\rangle +t\langle -5,6,-2\rangle\) and comparing each component, we obtain:

\[\begin{aligned} x & =3-5t\\ y & =1+6t\\ z & =-2-2t \end{aligned}\]

Question (iii)

\[\frac{x-3}{-5} =\frac{y-1}{6} =\frac{z+2}{-2}\]

Q4: Let \(ABCD\) be a parallelogram. If \(A( 3,2,\ -5)\), \(B( 4,1,0)\) and \(C( 1,1,4)\) are three vertices of parallelogram. Find point D.

Solution

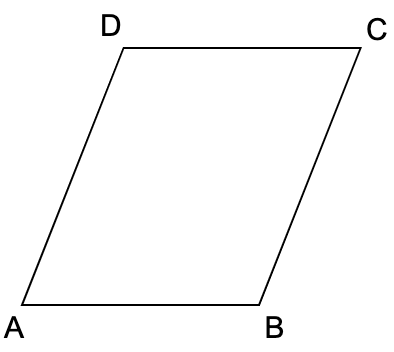
Diagram for solution of Question 4

\(\overrightarrow{AD} \vert\vert\overrightarrow{BC}\) or \(\overrightarrow{AB} \vert\vert\overrightarrow{CD}\)

\(\overrightarrow{AD} =\alpha \overrightarrow{BC}\) where \(\alpha =1\) (Same magnitude and direction)

\[\begin{aligned} \overrightarrow{AD} & =\overrightarrow{BC}\\ \overrightarrow{OD} -\overrightarrow{OA} & =\overrightarrow{OC} -\overrightarrow{OB}\\ \overrightarrow{OD} -\langle 3,2,-5\rangle & =\langle 1,1,4\rangle -\langle 4,1,0\rangle \\ \overrightarrow{OD} & =\langle 0,2,-1\rangle \end{aligned}\] \[\therefore D=( 0,2,-1)\]

Q5: Let \(\overrightarrow{OP} =\underset{\sim }{i} +3\underset{\sim }{j} -7\underset{\sim }{k}\) and \(\overrightarrow{OQ} =5\underset{\sim }{i} -2\underset{\sim }{j} +4\underset{\sim }{k}\)

(i) Find the unit vector in the direction of \(\overrightarrow{PQ}\)

(ii) Find the direction cosines of \(\overrightarrow{PQ}\)

(iii)Find the vector of magnitude 5 in the direction of \(\overrightarrow{QP}\) in polar form

Solution

Question (i)

\[\begin{aligned} \overrightarrow{PQ} & =\overrightarrow{OQ} -\overrightarrow{OP}\\ & =\langle 5,-2,4\rangle -\langle 1,3,-7\rangle \\ & =\langle 4,-5,11\rangle \end{aligned}\] \[\begin{aligned} \overrightarrow{PQ} & =\frac{\overrightarrow{PQ}}{| \overrightarrow{PQ}| }\\ & =\frac{\langle 4,-5,11\rangle }{\sqrt{( 4)^{2} +( -5)^{2} +( 11)^{2}}}\\ & =\mathbf{\frac{1}{9\sqrt{2}} \langle 4,-5,11\rangle } \end{aligned}\]

Question (ii)

Comparing each component, we obtain:

For component \(\underset{\sim }{i}\), \(\cos \alpha =\frac{4}{9\sqrt{2}}\)
For component \(\underset{\sim }{j}\), \(\cos \beta =\frac{-5}{9\sqrt{2}}\)
For component \(\underset{\sim }{k}\), \(\cos \gamma =\frac{11}{9\sqrt{2}}\)

Question (iii)

\[\begin{aligned} \cos \alpha =\frac{4}{9\sqrt{2}} & \Longrightarrow \ \alpha =71.68^\circ \\ \ \cos \beta =\frac{-5}{9\sqrt{2}} & \Longrightarrow \ \beta =113.13^\circ \\ \cos \gamma =\frac{11}{9\sqrt{2}} & \Longrightarrow \ \gamma =30.20^\circ \end{aligned}\]

Direction \(\overrightarrow{PQ}\) is in the direction of its unit vector, \(\langle \cos( 71.68^\circ ) ,\cos( 113.13^\circ ) ,\cos( 30.20^\circ ) \rangle\).

Direction \(\overrightarrow{QP}\) is in the direction of its unit vector, \(\begin{array} \langle \cos( 180-71.68^\circ ) ,\cos( 180-113.13^\circ ) ,\cos( 180-30.20^\circ ) \rangle \\ =\langle \cos( 108.32^\circ ) ,\cos( 66.87^\circ ) ,\cos( 149.80^\circ ) \rangle \end{array}\)

Vector of magintude 5 in the direction \(\overrightarrow{QP}\) is \(5\langle \cos( 108.32^\circ ) ,\cos( 66.87^\circ ) ,\cos( 149.80^\circ ) \rangle\).

Q6: Let \(A( 1,2)\) and \(B( 3,4)\)

(i) Find the vector equation of the line \(L\) passing points \(A\) and \(B\).

(ii) Sketch the line for \(t=0:1:5\) and indicate its direction and initial point.

Solution

Question (i)

Direction of vector is parallel with \(\overrightarrow{AB} =\overrightarrow{OB} -\overrightarrow{OA} =\langle 3,4\rangle -\langle 1,2\rangle =\mathbf{\langle 2,2\rangle }\)

Vector equation of line \(L\) is \(\underset{\sim }{r} =\underset{\sim }{a} +t\underset{\sim }{v} =\mathbf{\langle 1,2\rangle +t\langle 2,2\rangle }\)

Question (ii)

\(t\)	\(\underset{\sim }{r}\)
0	\(\langle 1,2\rangle\)
1	\(\langle 3,4\rangle\)
2	\(\langle 5,6\rangle\)
3	\(\langle 7,8\rangle\)
4	\(\langle 9,10\rangle\)
5	\(\langle 11,12\rangle\)

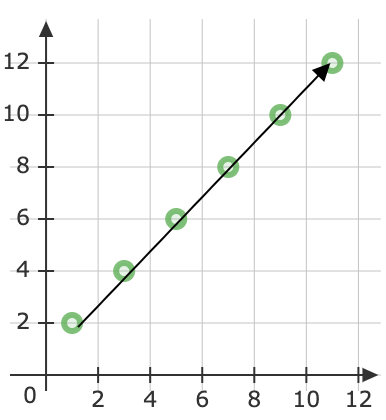
Graph for solution of Question 6(ii)

Q7: If a unit vector \(\vec{a}\) makes angles \(\frac{\pi }{3}\) with \(i\), \(\frac{\pi }{4}\) with \(j\) and acute angle \(\theta\) with \(k\) then find \(\theta\) and hence components of \(\vec{a}\).

Solution

Let \(\alpha ,\beta ,\gamma\) to represent angles of \(\vec{a}\), and \(\vec{a} =a_{1} i+a_{2} j+a_{3} k\).

\[\begin{aligned} \cos \alpha & =\frac{a_{1}}{| a_{1}| }\\ \cos\left(\frac{\pi }{3}\right) & =\frac{a_{1}}{1}\\ a_{1} & =\frac{1}{2} \end{aligned}\] \[\begin{aligned} \cos \beta & =\frac{a_{2}}{| a_{2}| }\\ \cos\left(\frac{\pi }{4}\right) & =\frac{a_{1}}{1}\\ a_{1} & =\frac{1}{\sqrt{2}} \end{aligned}\] \[\begin{aligned} \cos \gamma & =\frac{a_{3}}{| a_{3}| }\\ \cos \theta & =\frac{a_{3}}{1}\\ a_{3} & =\cos \theta \end{aligned}\] \[\therefore \ \vec{a} =\frac{1}{2} i+\frac{1}{\sqrt{2}} j+\cos \theta k\] \[\begin{aligned} | \vec{a}| & =\sqrt{\left(\frac{1}{2}\right)^{2} +\left(\frac{1}{\sqrt{2}}\right)^{2} +(\cos \theta )^{2}}\\ 1 & =\sqrt{\frac{1}{4} +\frac{1}{2} +\cos^{2} \theta }\\ 1 & =\frac{3}{4} +\cos^{2} \theta \\ \cos^{2} \theta & =\frac{1}{4}\\ \cos \theta & =\pm \frac{1}{2}\\ \theta & =60^\circ \ or\ 120^\circ \end{aligned}\] \[\therefore \ \vec{a} =\frac{1}{2} i+\frac{1}{\sqrt{2}} j+\frac{1}{2} k\ \quad or\quad \vec{a} =\frac{1}{2} i+\frac{1}{\sqrt{2}} j-\frac{1}{2} k\]

Q8: If \(\vec{a}\) is a unit vector and \((\vec{x} -\vec{a}) \cdot (\vec{x} +\vec{a}) =8\), then find \(| \vec{x}|\).

Solution

Since \(\vec{a}\) is a unit vector, \(\vert \vec{a}\vert =1\).

\[\begin{aligned} (\vec{x} -\vec{a}) \cdot (\vec{x} +\vec{a}) & =8\\ \vec{x} \cdot \vec{x} +\vec{x} \cdot \vec{a} -\vec{a} \cdot \vec{x} -\vec{a} \cdot \vec{a} & =8\\ | \vec{x}| ^{2} -| \vec{a}| ^{2} & =8\\ | \vec{x}| ^{2} -1 & =8\\ | \vec{x}| ^{2} & =9\\ | \vec{x}| & =3 \end{aligned}\]

Note that magnitude of vector is non-negative.