Tutorial 10: Multiple Integrals
Q1: Evaluate each of the following integrals over the given region \(D\).
(a) \(\int \int _{D} e^{\frac{x}{y}} \ dA, \qquad D=\left\{( x,y) \ |\ 1\leqslant y\leqslant 2,\ y\leqslant x\leqslant y^{3}\right\}\)
(b) \(\int \int _{D} 4xy-y^{3} \ dA\), \(D\) is the region bounded by \(y=\sqrt{x}\) and \(y=x^{3}\)
Solution
Question (a)
\[\begin{aligned} \int \int _{D} e^{\frac{x}{y}} \ dA\ & =\int _{1}^{2}\int _{y}^{y^{3}} e^{\frac{x}{y}} \ dxdy\\ & =\int _{1}^{2}\left. ye^{xy}\right| _{y}^{y^{3}} \ dy\\ & =\int _{1}^{2}\left( ye^{y^{4}} -ye^{y^{2}}\right) \ dy\\ & =\left. \left(\frac{1}{2} e{^{y}}^{2} -\frac{1}{2} y^{2} e^{1}\right)\right| _{1}^{2}\\ & =\mathbf{\frac{1}{2} e^{4} -2e^{1}} \end{aligned}\]Question (b)
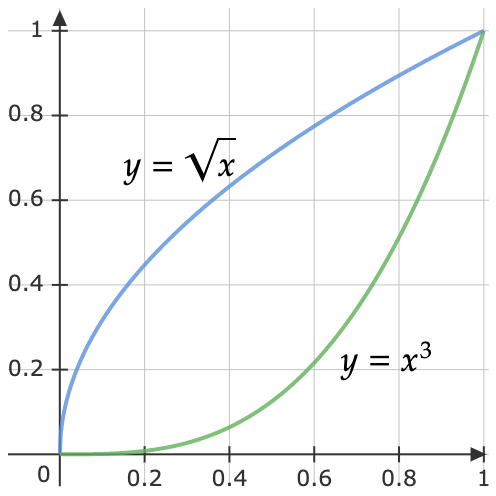
Two inequalities:
\[0\leqslant x\leqslant 1 \qquad x^{3} \leqslant y\leqslant \sqrt{x}\] \[\begin{aligned} \int \int _{D} 4xy-y^{3} \ dA & =\int _{0}^{1}\int _{x^{3}}^{\sqrt{x}} 4xy-y^{3} \ dydx\\ & =\int _{0}^{1}\left. \left( 2xy^{2} -\frac{1}{4} y^{4}\right)\right| _{x^{3}}^{\sqrt{x}} dx\\ & =\int _{0}^{1} 2x^{2} -\frac{1}{4} x^{2} -2x^{7} +\frac{1}{4} x^{12} dx\\ & =\int _{0}^{1}\frac{1}{4} x^{12} -2x^{7} +\frac{7}{4} x^{2} dx\\ & =\left. \left(\frac{1}{52} x^{13} -\frac{2}{8} x^{8} +\frac{7}{12} x^{3}\right)\right| _{0}^{1}\\ & =\frac{1}{52} -\frac{2}{8} +\frac{7}{24}\\ & =\mathbf{\frac{55}{156}} \end{aligned}\]Q2: Evaluate \(\int _{0}^{8}\int _{\sqrt[3]{y}}^{2}\sqrt{x^{4} +1} \ dxdy\).
Solution
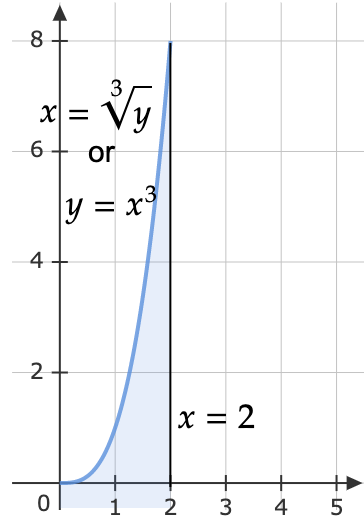
Two inequalities:
\[\sqrt[3]{y} \leqslant x\leqslant 2 \qquad 0\leqslant y\leqslant 8\]Reversing the inequalities:
\[0\leqslant x\leqslant 2 \qquad 0\leqslant y\leqslant x^{3}\] \[\begin{aligned} \int _{0}^{8}\int _{\sqrt[3]{y}}^{2}\sqrt{x^{4} +1} \ dxdy & =\int _{0}^{2}\int _{0}^{x^{3}}\sqrt{x^{4} +1} \ dydx\\ & =\int _{0}^{2}\left. y\sqrt{x^{4} +1}\right| _{0}^{x^{3}} dx\\ & =\int _{0}^{2} x^{3}\sqrt{x^{4} +1} \ dx \end{aligned}\]Let \(u=x^{4} +1\), \(du=4x^{3} dx\). Therefore, \(x^{3} dx=\frac{1}{4} du\).
Thus, the lower bound is now \(u=0^{4} +1=1\) and upper bound is now \(u=2^{4} +1=17\).
Hence,
\[\begin{aligned} \int _{0}^{2} x^{3}\sqrt{x^{4} +1} \ dx & =\int _{1}^{17}\frac{1}{4}\sqrt{u} \ du\\ & =\left. \frac{1}{4}\frac{u^{\frac{3}{2}}}{\frac{3}{2}}\right| _{1}^{17}\\ & =\frac{1}{6}\left( 17^{\frac{3}{2}} -1^{\frac{3}{2}}\right)\\ & =\mathbf{\frac{1}{6}\left( 17\sqrt{17} -1\right)} \end{aligned}\]Q3: Evaluate the following integral \(\int \int \int\limits _{B} 8xyz\ dV\), \(B=[ 2,3] \times [ 1,2] \times [ 0,1]\).
Solution
\[\begin{aligned} \int \int \int\limits _{B} \ 8xyz\ \ dV & =\int\limits _{1}^{2}\int\limits _{2}^{3}\int\limits _{0}^{1} 8xyz\ dz\ dx\ dy\\ & =\int\limits _{1}^{2}\int\limits _{2}^{3}\left. 4xyz^{2}\right| _{0}^{1} \ dx\ dy\\ & =\int\limits _{1}^{2}\int\limits _{2}^{3} 4xy\ dx\ dy\\ & =\int\limits _{1}^{2}\left. 2x^{2} y\right| _{2}^{3} \ \ dy\\ & =\int\limits _{1}^{2}\left( 2\left( 3^{2}\right) y-2( 2)^{2} y\right) \ dy\\ & =\int\limits _{1}^{2} 10y\ dy\\ & =\left. 5y^{2}\right| _{1}^{2}\\ & =5( 2)^{2} -5( 1)^{1}\\ & =\mathbf{15} \end{aligned}\]Q4: Determine the volume of the region that lies behind the plane \(x+y+z=8\) and in front of the region in the yz-plane that is bounded by \(z=\frac{3}{2}\sqrt{y}\) and \(z=\frac{3}{4} y\).
Solution
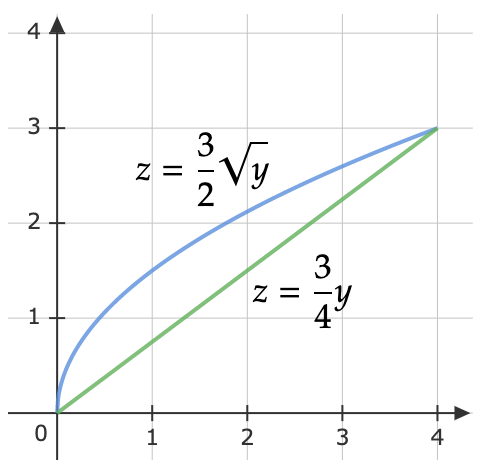
Limit of the variable:
\[0\leqslant y\leqslant 4\] \[\frac{3}{4} y\leqslant z\leqslant \frac{3}{2}\sqrt{y}\] \[0\leqslant x\leqslant 8-y-z\]Therefore the volume:
\[\begin{aligned} \int \int \int\limits _{B} \ \ \ dV & =\int \int\limits _{D}\left[\int\nolimits _{0}^{8-y-z} dx\right] \ dA\\ & =\int\limits _{0}^{4}\int\nolimits _{\frac{3}{4} y}^{\frac{3}{2}\sqrt{y}}( 8-y-z) \ dz\ dy\\ & =\int\limits _{0}^{4}\left. 8z-yz-\frac{z^{2}}{2}\right| _{\frac{3}{4} y}^{\frac{3}{2}\sqrt{y}} dy\\ & =\int\limits _{0}^{4}\left[ 8\left(\frac{3}{2}\sqrt{y}\right) -y\left(\frac{3}{2}\sqrt{y}\right) -\frac{\left(\frac{3}{2}\sqrt{y}\right)^{2}}{2}\right] -\left[ 8\left(\frac{3}{4} y\right) -y\left(\frac{3}{4} y\right) -\frac{\left(\frac{3}{4} y\right)^{2}}{2}\right] \ dy\\ & =\int\nolimits _{0}^{4}\left( 12y^{\frac{1}{2}} -\frac{3}{2} y^{\frac{3}{2}} -\frac{9}{8} y-6y+\frac{3}{4} y^{2} +\frac{9}{32} y^{2}\right) \ dy\\ & =\int\nolimits _{0}^{4}\left(\frac{33}{32} y^{2} -\frac{3}{2} y^{\frac{3}{2}} -\frac{57}{8} y+12y^{\frac{1}{2}}\right) \ dy\\ & =\left. \frac{33}{96} y^{3} -\frac{6}{10} y^{\frac{5}{2}} -\frac{57}{16} y^{2} +8y^{\frac{3}{2}}\right| _{0}^{4}\\ & =\frac{33}{96}( 4)^{3} -\frac{6}{10}( 4)^{\frac{5}{2}} -\frac{57}{16}( 4)^{2} +8( 4)^{\frac{3}{2}}\\ & =\mathbf{\frac{49}{5}} \end{aligned}\]Q5: Find the volume of the region bounded by the paraboloid \(z=4-4x^{2} -4y^{2}\) and the plane \(z=0\).
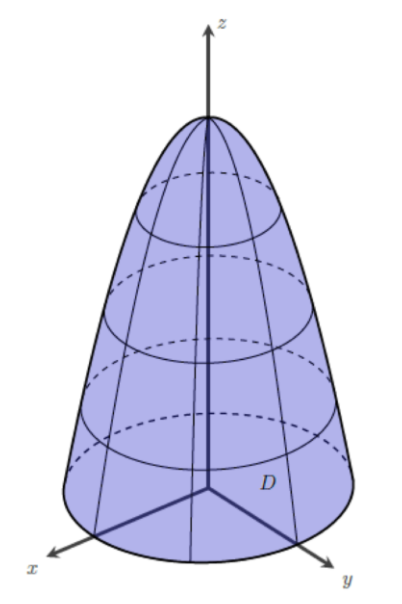
Solution
The region \(D\) is on xy-plane, so \(z=0\).
Given \(z=0\),
\[\begin{aligned} z & =4-4x^{2} -4y^{2}\\ 0 & =4-4x^{2} -4y^{2}\\ 4x^{2} +4y^{2} & =4\\ x^{2} +y^{2} & =1 \end{aligned}\]\(x^{2} +y^{2} =1\) is a circle equation with \(r=1\).
Since \(D\) is a circular disk, the integration will be in polar coordinate.
The limit: \(0\leqslant \theta \leqslant 2\pi \qquad 0\leqslant r\leqslant 1\)
\[\begin{aligned} V & =\int \int\limits _{D}\left( 4-4x^{2} -4y^{2}\right) dA\\ & =\int \int\limits _{D} 4\left( 1-\left( x^{2} +y^{2}\right)\right) dA\\ & =\int _{0}^{2\pi }\int\nolimits _{0}^{1} 4\left( 1-r^{2}\right) r\ drd\theta \\ & =4\int _{0}^{2\pi } d\theta \ \int _{0}^{1}\left( r-r^{3}\right) \ dr\\ & =4\ \cdot \ \theta | _{0}^{2\pi } \ \cdot \ \left. \frac{r^{2}}{2} -\frac{r^{4}}{4}\right| _{0}^{1}\\ & =4\cdot ( 2\pi ) \cdot \left(\frac{1}{2} -\frac{1}{4}\right)\\ & = 8\pi \left(\frac{1}{4}\right)\\ & =\mathbf{2\pi } \end{aligned}\]Q6: Evaluate the following integral
\[\int \int \int xy^{2}\cos( xyz) \ dx\ dy\ dz;\ B=[ 0,\pi ] \times \left[ 0,\frac{1}{2}\right] \times [ 0,1]\]Solution
\[\int _{0}^{\pi }\int\nolimits _{0}^{\frac{1}{2}}\int\nolimits _{0}^{1} xy^{2}\cos( xyz) \ dz\ dy\ dx\]Let \(u=xyz\), \(du=xy\ dz\Longrightarrow \ dz=\frac{du}{xy}\),
\[\begin{aligned} \int xy^{2}\cos( xyz) \ dz & =\int xy^{2}\cos( u) \ \frac{du}{xy}\\ & =\int y\ \cos( u) \ du\\ & =y\sin( u)\\ & =y\sin( xyz) \end{aligned}\]Subtituting back to the original integral,
\[\begin{aligned} \int _{0}^{\pi }\int\nolimits _{0}^{\frac{1}{2}}\int\nolimits _{0}^{1} xy^{2}\cos( xyz) \ dz\ dy\ dx & =\int _{0}^{\pi }\int\nolimits _{0}^{\frac{1}{2}} y\sin( xyz)| _{z=0}^{z=1} \ dy\ dx\\ & =\int _{0}^{\pi }\int\nolimits _{0}^{\frac{1}{2}}[ y\sin( xy) -y\sin( 0)] \ dy\ dx\\ & =\int _{0}^{\pi }\int\nolimits _{0}^{\frac{1}{2}} y\sin( xy) \ dy\ dx\\ & =\int _{0}^{\frac{1}{2}}\left. -\frac{y}{y}\cos( xy)\right| _{x=0}^{x=\pi } \ \ dy\\ & =\int _{0}^{\frac{1}{2}}[ -\cos( \pi y) +\cos 0] \ \ dy\\ & =\int _{0}^{\frac{1}{2}}[ -\cos( \pi y) +1] \ \ dy\\ & =\left. -\frac{1}{\pi }\sin( \pi y) +y\right| _{0}^{\frac{1}{2}}\\ & =-\frac{1}{\pi }\sin\left(\frac{\pi }{2}\right) +\frac{1}{2} +\frac{1}{\pi }\sin 0\\ & =\mathbf{-\frac{1}{\pi } +\frac{1}{2}} \end{aligned}\]