Tutorial 2: Functions & Derivatives
Solving using MATLAB Solving using Python
Q1: Find \(y'\) for \((x-y)^2=x+y-1\) by using implicit differentiation.
Solution
\[\begin{aligned} \mathcal{D}(x-y)^2&=\mathcal{D}(x+y-1) \\ \mathcal{D}(x-y)^2&=\mathcal{D}(x)+\mathcal{D}(y)-\mathcal{D}(1) \\ 2(x-y)\mathcal{D}(x-y)&=1+y' \\ 2(x-y)(1-y')&=1+y' \\ 2(x-y)-2(x-y)y'&=1+y' \\ -2(x-y)y'-y'&=1-2(x-y) \\ y'[-2(x-y)-1]&=1-2(x-y) \\ y'&=\frac{1-2(x-y)}{-2(x-y)-1} \\ y'&=\boldsymbol{\frac{2y-2x+1}{2y-2x-1}} \end{aligned}\]Q2: Implicit differentiation to find an equation of the tangent line to the curve \(5x^2+10xy^2+5y=20\) at point \((2,2)\).
Solution
\[\begin{aligned} \mathcal{D}(5x^2+10xy^2+5y)&=\mathcal{D}(20) \\ 10x+10x(2y\cdot y')+y^2\cdot10+5y'&=0 \\ 10x+20xy\cdot y'+10y^2+5y'&=0 \\ (20xy+5)y'&=-10y^2-10x \\ y'&=\frac{-10y^2-10x}{20xy+5} \end{aligned}\]At point \((2,2)\), \(y'=\frac{-10(2)^2-10(2)}{20(2)(2)+5}=-\frac{12}{17}\)
Knowing \(y=mx+c\),
\[2=-\frac{12}{17}(2)+c \rightarrow c=\frac{58}{17}\] \[\therefore \text{Tangent Line: }\boldsymbol{y=-\frac{12}{17}x+\frac{58}{17}}\]Q3: \(y\cos{x}=1+\sin{(xy)}\). Find \(\frac{dy}{dx}\) by implicit differentiation.
Solution
\[\begin{aligned} y\cos{x}&=1+\sin{(xy)} \\ y(-\sin{x})+(\cos{x})y'&=\cos{(xy)}\cdot(xy'+y) \\ -y\sin{x}+y'\cos{x}&=(xy'+y)\cos{(xy)} \\ y'&=\boldsymbol{\frac{y\cos{(xy)}+y\sin{x}}{\cos{x}-x\cos{xy}}} \end{aligned}\]Q4: Find \(\frac{dy}{dx}\) by implicit differentiation \(4\cos{x}\sin{y}=1\).
Solution
\[\begin{aligned} 4\cos{x}\sin{y}&=1\\ (4\cos{x})\cdot(\cos{y})\cdot y'+(\sin{y})\cdot(-4\sin{x})&=0 \\ y'&=\frac{4\sin{x}\sin{y}}{4\cos{x}\cos{y}} \\ &= \boldsymbol{\tan{x}\tan{y}} \end{aligned}\]Q5: An open box is to be made from cutting a square from each corner of a 12 in by 12 in piece of metal and then folding up the sides. What size square should be cut from each corner to produce a box of maximum volume?
Solution
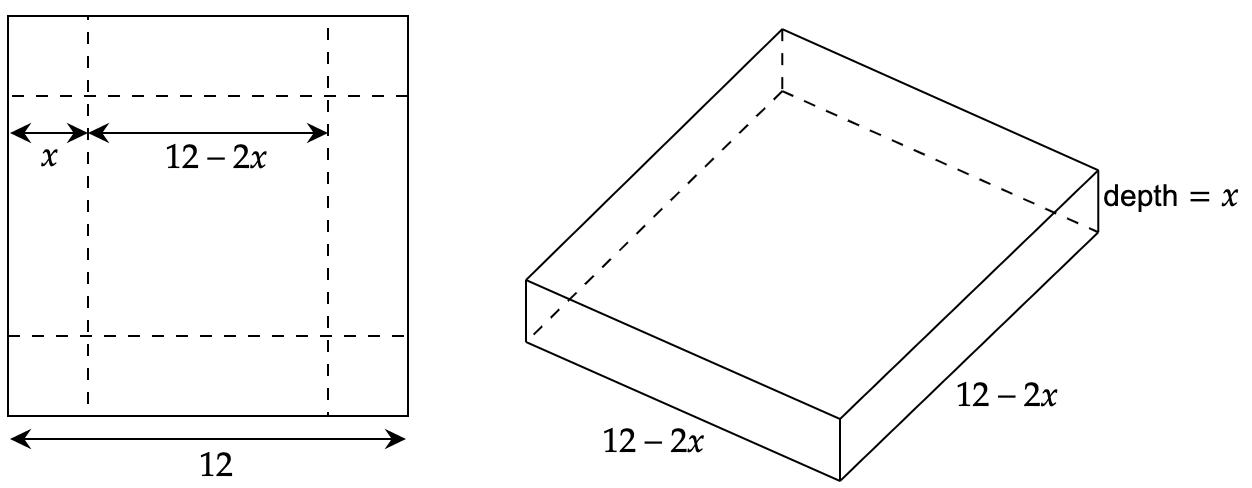
The volume is to be maximized, \(V=lwh=x(12-2x)(12-2x)=4x^3-48x^2+144x\).
\[\begin{aligned} V(x)&=4x^3-48x^2+144x \\ V'(x)&=12x^2-96x+144 \end{aligned}\]The critical point can be calculate such that, \(V'(x)=0\).
\[\begin{aligned} 0&=12x^2-96x+144 \\ 0&=12(x^2-8x+12) \\ 0&=12(x-2)(x-6) \\ \therefore x&=2,6 \end{aligned}\]When \(x=2\), \(V(2)=128\).
When \(x=6\), \(V(6)=0\).
Thus, when \(x=2\), the maximum volume is 128 in\(^3\). To prove that, using second derivation,
\(V''(x)=24x-96\).
When \(x=2\), \(V''(2) < 0\) (Maximum Volume)
When \(x=6\), \(V''(6) > 0\) (Minimum Volume)
Thus, \(x=2\).
Q6: We are going to fence in a rectangular field. If we look at the field from above the cost of the vertical sides are RM 10/ft, the cost of the bottom is RM2/ft and the cost of the top is RM 7 /ft. If we have RM 700 determind the dimensions of the field that will maximize the enclosed area.
Solution
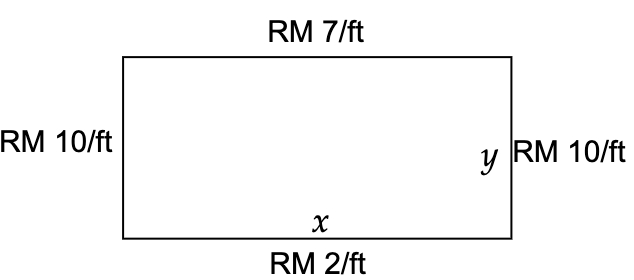
We have RM 700, therefore \(700=10y+2x+10y+7x=20y+9x\).
In terms of \(y\), \(y=35-\frac{9}{20}x\).
Since \(A=xy\), plugging in yields \(A(x)=x\left(35-\frac{9}{20}x\right)\).
The critical point can be calculate such that, \(V'(x)=0\).
\[\begin{aligned} A'(x) &= 35-\frac{9}{10}(x) \\ 0&=35-\frac{9}{10}(x) \\ \therefore x&=\frac{350}{9} \end{aligned}\]The second derivation,
\(A''(x)=-\frac{9}{10}\).
This means that the second derivative always negative and so \(A(x)\) will always be concave down and so the single critical point. Therefore the value obtained in \(A'(x)\) must be the value that yield maximum area.
Substituting \(x=\frac{350}{9}\) into the equation of \(y\), \(y=35-\frac{9}{20}\left(\frac{350}{9}\right)=\frac{35}{2}\).
Thus, the final dimension is, \(\boldsymbol{x=\frac{350}{9}, y=\frac{35}{2}}\).