Tutorial 7: Engineering Applications of Matrices and Vectors
Q1: An electrical engineer supervises the production of three types of electrical components. Three kinds of materials are; metal, plastic and rubber – are required for production. The amounts needed to produce each component are
| Component | Metal (g/component) | Plastic (g/component) | Rubber (g/component) |
|---|---|---|---|
| 1 | 15 | 0.25 | 1.0 |
| 2 | 17 | 0.33 | 1.2 |
| 3 | 19 | 0.42 | 1.6 |
If totals of 2.12, 0.0434 and 0.164 kg of metal, plastic and rubber respectively are available each day, how many components can be produced per day?
Solution
\[\begin{aligned} \begin{bmatrix} 15 & 17 & 19\\ 0.25 & 0.33 & 0.42\\ 1 & 1.2 & 1.6 \end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3} \end{bmatrix} & =\begin{bmatrix} 2120\\ 43.4\\ 164 \end{bmatrix} \end{aligned}\] \[D=\begin{vmatrix} 15 & 17 & 19\\ 0.25 & 0.33 & 0.42\\ 1 & 1.2 & 1.6 \end{vmatrix} =0.13\] \[D_{x_{1}} =\begin{vmatrix} 2120 & 17 & 19\\ 43.4 & 0.33 & 0.42\\ 164 & 1.2 & 1.6 \end{vmatrix} =2.6\] \[D_{x_{2}} =\begin{vmatrix} 15 & 2120 & 19\\ 0.25 & 43.4 & 0.42\\ 1 & 164 & 1.6 \end{vmatrix} =5.2\] \[D_{x_{3}} =\begin{vmatrix} 15 & 17 & 2120\\ 0.25 & 0.33 & 43.4\\ 1 & 1.2 & 164 \end{vmatrix} =7.8\] \[\begin{aligned} x_{1} & =\frac{D_{x_{1}}}{D}\\ & =\frac{2.6}{0.13}\\ & =\mathbf{20} \end{aligned}\] \[\begin{aligned} x_{2} & =\frac{D_{x_{2}}}{D}\\ & =\frac{5.2}{0.13}\\ & =\mathbf{40} \end{aligned}\] \[\begin{aligned} x_{3} & =\frac{D_{x_{3}}}{D}\\ & =\frac{7.8}{0.13}\\ & =\mathbf{60} \end{aligned}\]Q2: A civil engineer involved in construction requires 4800, 5800 and 5700 m\(^3\) of sand, fine gravel and coarse gravel respectively for building a project. There are three pits from which these materials can be obtained. The composition of these pits is
| Sand % | Fine Gravel % | Coarse Gravel % | |
|---|---|---|---|
| Pit 1 | 52 | 30 | 18 |
| Pit 2 | 20 | 50 | 30 |
| Pit 3 | 25 | 20 | 55 |
How many cubic meters must be hauled from each pit in order to meet the engineer’s needs?
Solution
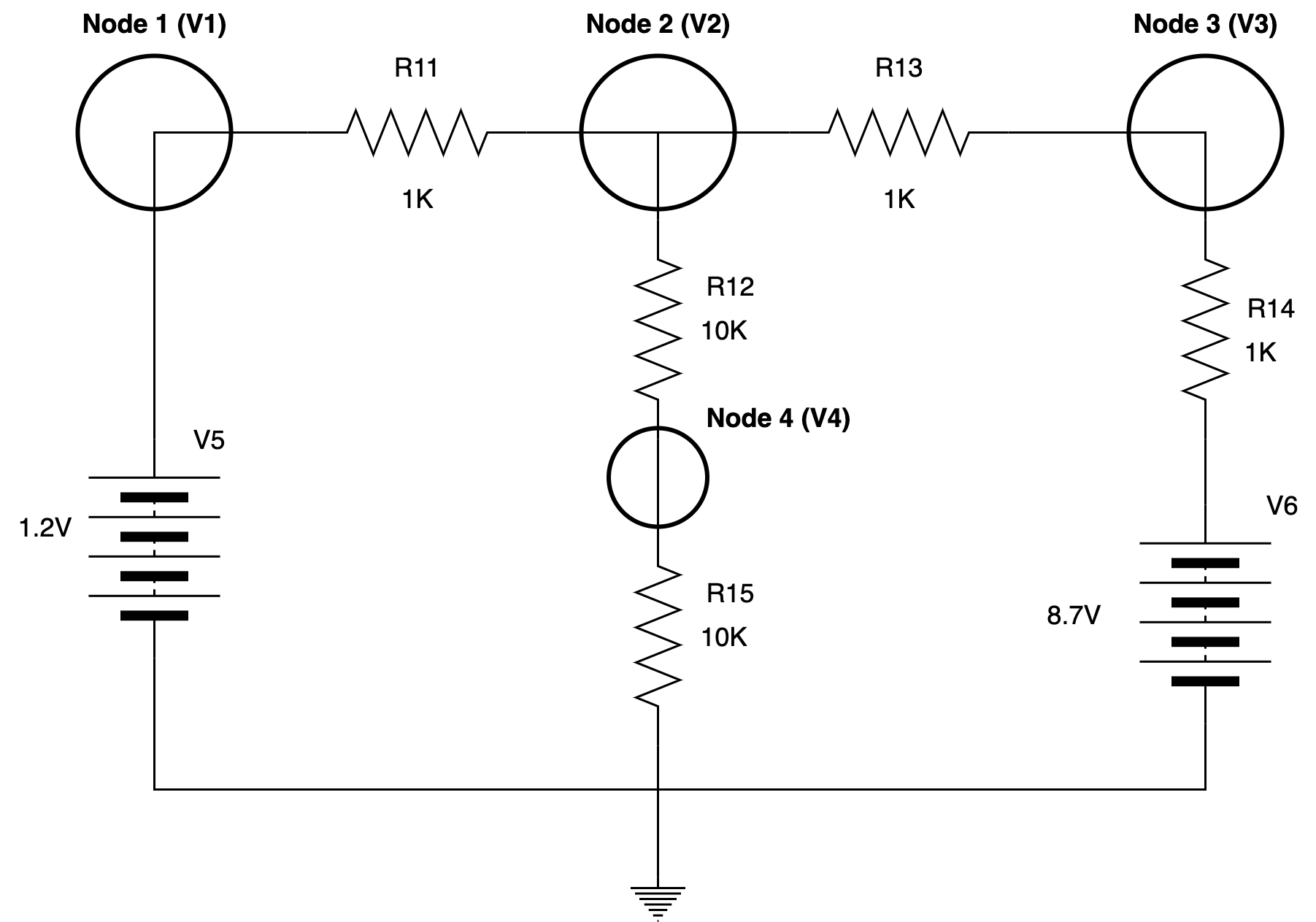
\[\begin{aligned} \begin{bmatrix} 0.52 & 0.30 & 0.18\\ 0.20 & 0.50 & 0.30\\ 0.25 & 0.20 & 0.55 \end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3} \end{bmatrix} & =\begin{bmatrix} 4800\\ 5800\\ 5700 \end{bmatrix} \end{aligned}\] \[D=\begin{vmatrix} 0.52 & 0.30 & 0.18\\ 0.20 & 0.50 & 0.30\\ 0.25 & 0.20 & 0.55 \end{vmatrix} =0.086\] \[D_{x_{1}} =\begin{vmatrix} 4800 & 0.30 & 0.18\\ 5800 & 0.50 & 0.30\\ 5700 & 0.20 & 0.55 \end{vmatrix} =344.5\] \[D_{x_{2}} =\begin{vmatrix} 0.52 & 4800 & 0.18\\ 0.20 & 5800 & 0.30\\ 0.25 & 5700 & 0.55 \end{vmatrix} =613.3\] \[D_{x_{3}} =\begin{vmatrix} 0.52 & 0.30 & 4800\\ 0.20 & 0.50 & 5800\\ 0.25 & 0.20 & 5700 \end{vmatrix} =444\] \[\begin{aligned} x_{1} & =\frac{D_{x_{1}}}{D}\\ & =\frac{344.5}{0.086}\\ & =\mathbf{4005.82} \end{aligned}\] \[\begin{aligned} x_{2} & =\frac{D_{x_{2}}}{D}\\ & =\frac{613.3}{0.086}\\ & =\mathbf{7131.40} \end{aligned}\] \[\begin{aligned} x_{3} & =\frac{D_{x_{3}}}{D}\\ & =\frac{444}{0.086}\\ & =\mathbf{5162.79} \end{aligned}\]Q3: By referring to the schematic below, find V1, V2, V3 and V4. Solve the problem using Cramer’s rule.
Solution
Node equations
Node Equation #1: \(V_{1} =1.2 \qquad \color{red} {\scriptsize{\triangleleft [\text{Since Node 1 directly connectted to source}]}}\)
Node Equation #2: \(\frac{V_{2} -1.2}{R_{11}} +\frac{V_{2} -V_{3}}{R_{13}} +\frac{V_{2} -V_{4}}{R_{12}} =0\)
Node Equation #3: \(\frac{V_{3} -V_{2}}{R_{13}} +\frac{V_{3} -8.7}{R_{14}} =0\)
Node Equation #4: \(\frac{V_{4} -V_{2}}{R_{12}} +\frac{V_{4} -0}{R_{15}} =0\)
Solving the node equations:
Substituting all values to Node Equation #2:
\[\begin{aligned} \frac{V_{2} -1.2}{1000} +\frac{V_{2} -V_{3}}{1000} +\frac{V_{2} -V_{4}}{10000} & =0\\ 10V_{2} -12+10V_{2} -10V_{3} +V_{2} -V_{4} & =0\\ 21V_{2} -10V_{3} -V_{4} & =12 \end{aligned} \tag{1}\]Substituting all values to Node Equation #3:
\[\begin{aligned} \frac{V_{3} -V_{2}}{1000} +\frac{V_{3} -8.7}{1000} & =0\\ V_{3} -V_{2} +V_{3} -8.7 & =0\\ -V_{2} +2V_{3} & =8.7 \end{aligned} \tag{2}\]Substituting all values to Node Equation #4:
\[\begin{aligned} \frac{V_{4} -V_{2}}{10000} +\frac{V_{4} -0}{10000} & =0\\ V_{4} -V_{2} +V_{4} & =0\\ -V_{2} +2V_{4} & =0 \end{aligned} \tag{3}\]Putting Equation (1) - (3) into matrix and solve for \(V_{2}\), \(V_{3}\), \(V_4\):
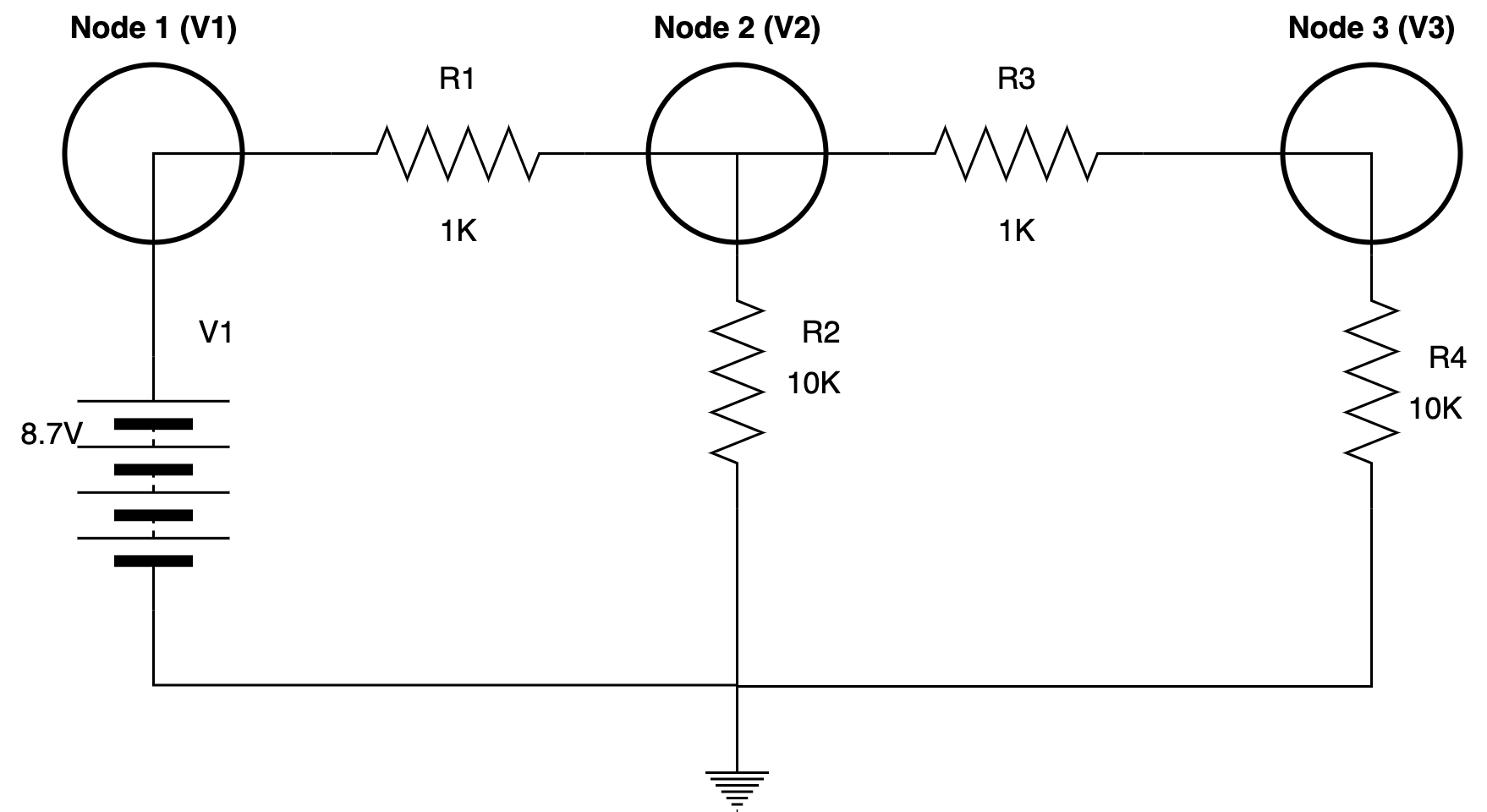
\[\begin{bmatrix} 21 & -10 & -1\\ -1 & 2 & 0\\ -1 & 0 & 2 \end{bmatrix}\begin{bmatrix} V_{2}\\ V_{3}\\ V_{4} \end{bmatrix} =\begin{bmatrix} 12\\ 8.7\\ 0 \end{bmatrix}\] \[D=\begin{vmatrix} 21 & -10 & -1\\ -1 & 2 & 0\\ -1 & 0 & 2 \end{vmatrix} =62\] \[D_{V_{2}} =\begin{vmatrix} 12 & -10 & -1\\ 8.7 & 2 & 0\\ 0 & 0 & 2 \end{vmatrix} =222\] \[D_{V_{3}} =\begin{vmatrix} 21 & 12 & -1\\ -1 & 8.7 & 0\\ -1 & 0 & 2 \end{vmatrix} =380.7\] \[D_{V_{4}} =\begin{vmatrix} 21 & -10 & 12\\ -1 & 2 & 8.7\\ -1 & 0 & 0 \end{vmatrix} =111\] \[\begin{aligned} V_{2} & =\frac{D_{V_{2}}}{D}\\ & =\frac{222}{62}\\ & =\mathbf{3.58\ V} \end{aligned}\] \[\begin{aligned} V_{3} & =\frac{D_{V_{3}}}{D}\\ & =\frac{380.7}{62}\\ & =\mathbf{6.14\ V} \end{aligned}\] \[\begin{aligned} V_{4} & =\frac{D_{V_{4}}}{D}\\ & =\frac{111}{62}\\ & =\mathbf{1.79\ V} \end{aligned}\] \[\therefore \ V_{1} =\mathbf{1.2\ V} ;\ \ V_{2} =\mathbf{3.58\ V} ;\ \ V_{3} =\mathbf{6.14\ V} ;\ \ V_{4} =\mathbf{1.79\ V}\]Q4: By referring to the schematic below, find V2, and V3. Solve the problem using Cramer’s rule.
Solution
Node equations
Node Equation #1: \(V_{1} =8.7 \qquad \color{red} {\scriptsize{\triangleleft [\text{Since Node 1 directly connectted to source}]}}\)
Node Equation #2: \(\frac{V_{2} -V_{1}}{R_{1}} +\frac{V_{2} -0}{R_{2}} +\frac{V_{2} -V_{3}}{R_{3}} =0\)
Node Equation #3: \(\frac{V_{3} -V_{2}}{R_{3}} +\frac{V_{3} -0}{R_{4}} =0\)
Solving the node equations:
Substituting all values to Node Equation #2:
\[\begin{aligned} \frac{V_{2} -8.7}{1000} +\frac{V_{2} -0}{10000} +\frac{V_{2} -V_{3}}{1000} & =0\\ 10V_{2} -87+V_{2} +10V_{2} -10V_{3} & =0\\ 21V_{2} -10V_{3} & =87 \end{aligned} \tag{1}\]Substituting all values to Node Equation #3:
\[\begin{aligned} \frac{V_{3} -V_{2}}{1000} +\frac{V_{3} -0}{10000} & =0\\ 10V_{3} -10V_{2} +V_{3} & =0\\ -10V_{2} +11V_{3} & =0 \end{aligned} \tag{2}\]Putting Equation (1) and (2) into matrix and solve for \(V_2\), \(V_3\):
\[\begin{bmatrix} 21 & -10\\ -10 & 11 \end{bmatrix}\begin{bmatrix} V_{2}\\ V_{3} \end{bmatrix} =\begin{bmatrix} 87\\ 0 \end{bmatrix}\] \[D=\begin{vmatrix} 21 & -10\\ -10 & 11 \end{vmatrix} =131\] \[D_{V_{2}} =\begin{vmatrix} 87 & -10\\ 0 & 11 \end{vmatrix} =957\] \[D_{V_{3}} =\begin{vmatrix} 21 & -87\\ -10 & 0 \end{vmatrix} =870\] \[\begin{aligned} V_{2} & =\frac{D_{V_{2}}}{D}\\ & =\frac{957}{131}\\ & =\mathbf{7.31\ V} \end{aligned}\] \[\begin{aligned} V_{3} & =\frac{D_{V_{3}}}{D}\\ & =\frac{870}{131}\\ & =\mathbf{6.64\ V} \end{aligned}\] \[\therefore \ V_{1} =\mathbf{8.7\ V} ;\ \ V_{2} =\mathbf{7.31\ V} ;\ \ V_{3} =\mathbf{6.64\ V}\]